Koppelgetriebe

Koppelgetriebe, oft auch "Gelenkgetriebe" oder umgangssprachlich "Hebelei" genannt, sind mechanische Strukturen mit Drehgelenken und Schubgelenken zum Übertragen von Bewegungen oder zum Führen von Punkten.

Gelenkgetriebe werden oft mit Kurvengetrieben, Servoantrieben oder Rädergetrieben kombiniert. Sie übertragen die Bewegung von einer Kurve auf das vielleicht entfernt arbeitende Werkzeug und damit an die Wirkstelle. Gleichzeitig übersetzen sie auch den Kurvenhub.

Bei komplexen Bewegungssteuerungen mit Koppelgetrieben geben wir die Bewegung in aller Regel an der Wirkstelle vor und rechnen mit unserer Software OPTIMUS MOTUS die resultierende Bewegung der Kurvenrolle oder des Servoantriebs aus.

Koppelgetriebe übertragen Bewegungen nichtlinear. Die Geschwindigkeit am Abtrieb ist also nicht proportional zur Antriebsgeschwindigkeit. Bei Synchronbewegungen und zur Gewährleistung der Kollisionsfreiheit bei komplexen Bewegungsabläufen ist es wichtig, das zu berücksichtigen.

Wegen der Nichtlinearitäten haben Koppelgetriebe auch für sich allein sehr interessante Eigenschaften und ermöglichen einfache, robuste und harmonisch laufende Lösungen für praktische Bewegungsaufgaben.

Beispiel:

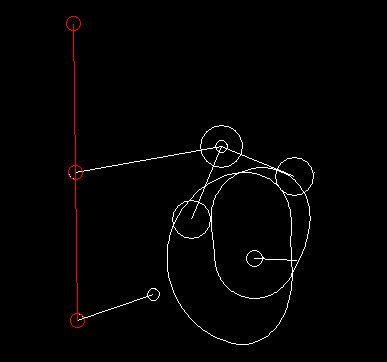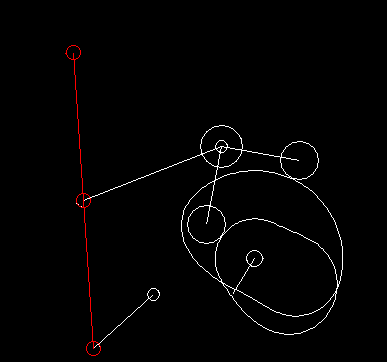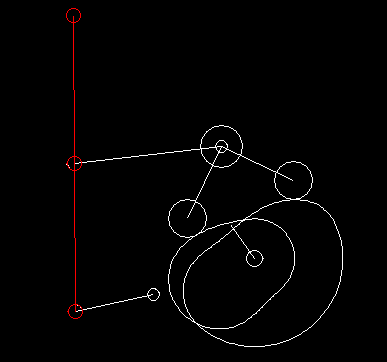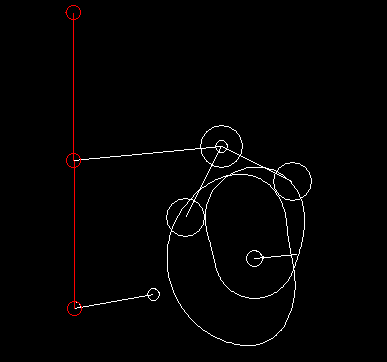
Die folgende Animation zeigt ein sechsgliedriges Koppelgetriebe (Gestell + 5 bewegte Teile), das in einer Verpackungsmaschine als Transportrechen eingesetzt wird. Es basiert auf einem Viergelenkgetriebe, das eine für den Transport geeignete, "brotförmige" Koppelkurve erzeugt, und einem angehängten Zweischlag, mit dem der Rechen in jeder Position waagerecht gehalten wird.

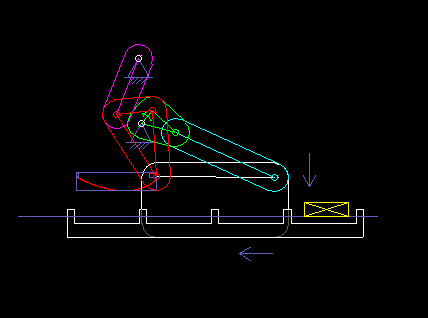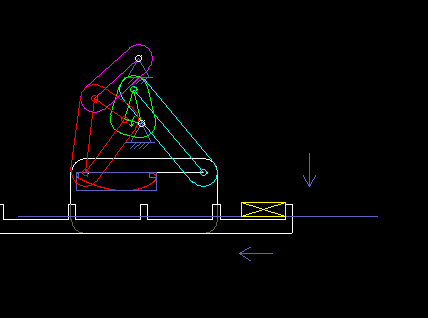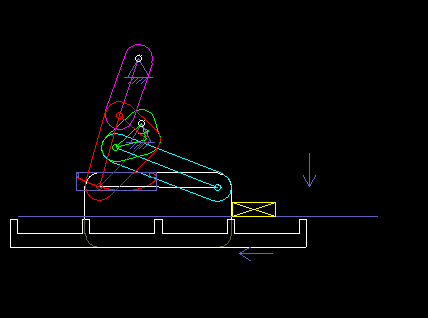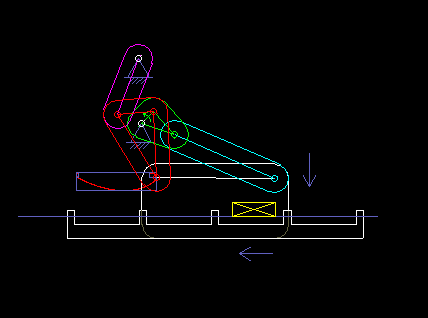
Als ich einmal die Produktion eines Süßwarenherstellers besuchte, fiel mir eine 50 Jahre alte Maschine auf, die keine Kurven und erst recht keine Servoantriebe enthielt und Schokolade verpackte. Solche Lösungen sind vielleicht nicht mehr zeitgemäß, aber sie zeigen, dass auch Koppelgetriebe allein komplexe Bewegungssteuerungen ermöglichen!

In Maschinen werden häufig Viergelenkgetriebe eingesetzt.

Servoantriebe werden oft mit Schubkurbeln kombiniert, um aus der umlaufenden Drehung des Servoantriebs bzw. des Getriebeausgangs eine hin- und hergehende Hubbewegung zu erzeugen.

In mechanischen Pressen werden teilweise mehrgliedrige Koppelgetriebe verwendet, um eine für den Umformprozess günstige Bewegung des Pressenstößels zu erzielen.

Aber auch aus dem täglichen Leben kennen Sie sicher selbst einige Beispiele für Gelenkgetriebe:

• Mechanik von Regenschirmen
• Hafenkräne
• Bagger
• Scharniere in Küchenschränken
• Scheibenwischer
• Spielzeug-Pantograph
• Gestänge an den Rädern einer Dampflok
• Mechanik an Cabriolet-Verdecken
• Bürolocher
• Astscheren
• Hubwagen

Unsere Themen bei Software, Beratung und Auslegung:

• Koppelgetriebeanalyse
• Kombination von Kurven, Servoantrieben und Koppelgetrieben
• Berechnungsmodule für Kinematik und Kinetostatik in C und ST
• Software-Quelltexte für kinematische Transformationen
• Digitale Zwillinge für Mechanismenstrukturen
• Koppelgetriebesynthese
• Spezielle Betrachtungen an Viergelenkgetrieben, Schubkurbelgetrieben, Kurbelschleifen, sechsgliedrigen Koppelgetrieben, mehrgliedrigen Koppelgetrieben

Direkt zu ...

• Viergelenkgetriebe
• Schubkurbel
• Berechnung (Analyse) von Gelenkgetrieben
• Kurven-Koppelgetriebe
• Koppelgetriebesynthese
• Verzweigungslagen
• Modulbibliothek
• Software
• Berechnung
• Kinematik

zur Startseite Nolte NC-Kurventechnik GmbH

> English version of this page

Viergelenkgetriebe

Das wohl bekannteste und am meisten untersuchte Koppelgetriebe schlechthin ist das ebene Viergelenkgetriebe, ein viergliedriges Koppelgetriebe ausschließlich mit Drehgelenken. Das Gestell zählt dabei als Glied mit.

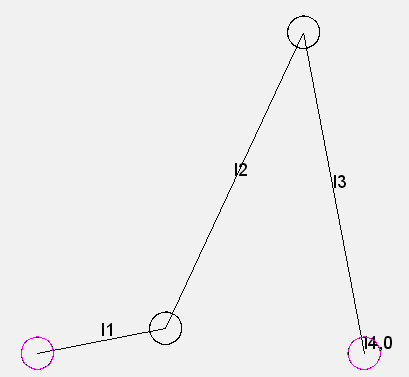
Viergelenkgetriebe werden zum Übertragen von Bewegungen und zum Führen von Punkten und Gliedern verwendet.

Sie bestechen durch ihre Einfachheit nach dem Grundsatz: je weniger bewegte Teile, desto besser.

Viergelenkgetriebe dienen oft als Basis für komplexere Mechanismenstrukturen.

Zu Zeiten der zeichnerischen Getriebeanalyse wurden Viergelenke oft als Ersatzgetriebe verwendet, um beispielsweise Eigenschaften von Kurvengetrieben zu untersuchen.

Sei lmin die kleinste, lmax die größte, und l' und l" die beiden anderen Getriebegliedlängen.

Nach dem Satz von Grashof ist das kürzeste Getriebeglied lmin gegenüber seinen Nachbarn umlauffähig, wenn gilt:

lmin+lmax < l'+l"

Die folgenden Animationen zeigen Beispiele für verschiedene Varianten von Viergelenkgetrieben.

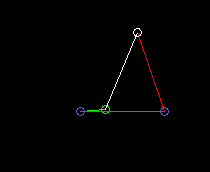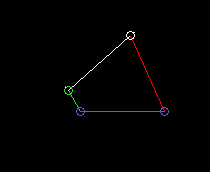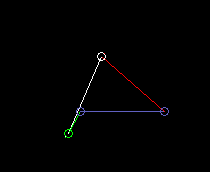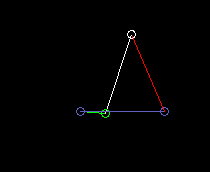
Antrieb = grün

Koppel = weiß

Abtrieb = rot

Gestell = blau

Kurbelschwinge:

lmin ist hier die Kurbellänge (grün), d.h. die Länge des angetriebenen Gliedes.

Doppelkurbel:

lmin ist hier die Länge des Gestells, also der Abstand von Kurbeldrehpunkt zu Schwingendrehpunkt.

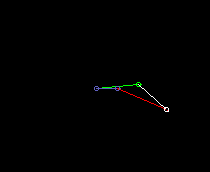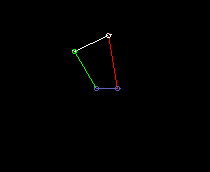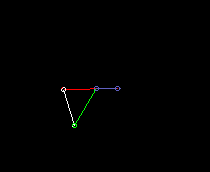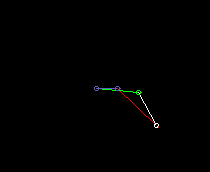
Doppelschwinge:

lmin ist hier die Koppellänge.

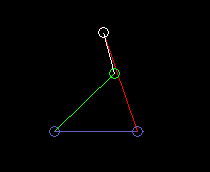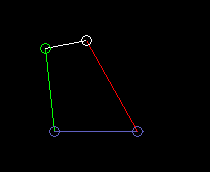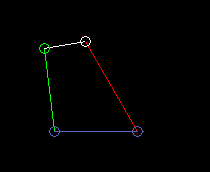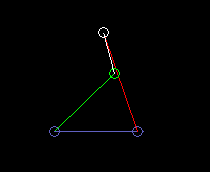
Innen schwingende Doppelschwinge (Totalschwinge):

lmax ist hier die Länge des Gestells. Und es ist lmin+lmax > l'+l".

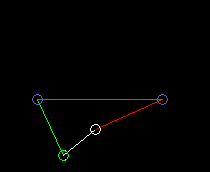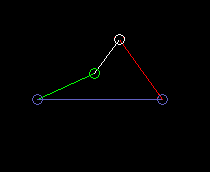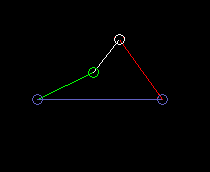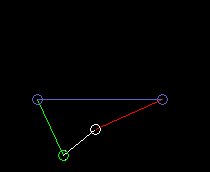
Die außen schwingende Doppelschwinge:

lmax ist dabei die Koppellänge.

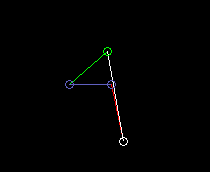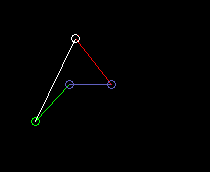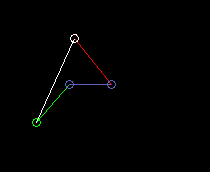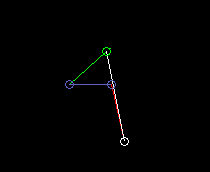
Werden die kinematischen Abmessungen passend gewählt, d.h. die Gliedlängen und die Lage des Koppelpunkts auf der Koppel, so wird der Koppelpunkt näherungsweise auf einer vorgegebenen Kurve geführt. Wegen der einfachen Getriebestruktur mit entsprechend wenigen Parametern sind aber nicht alle Kurven gleich gut annäherbar.

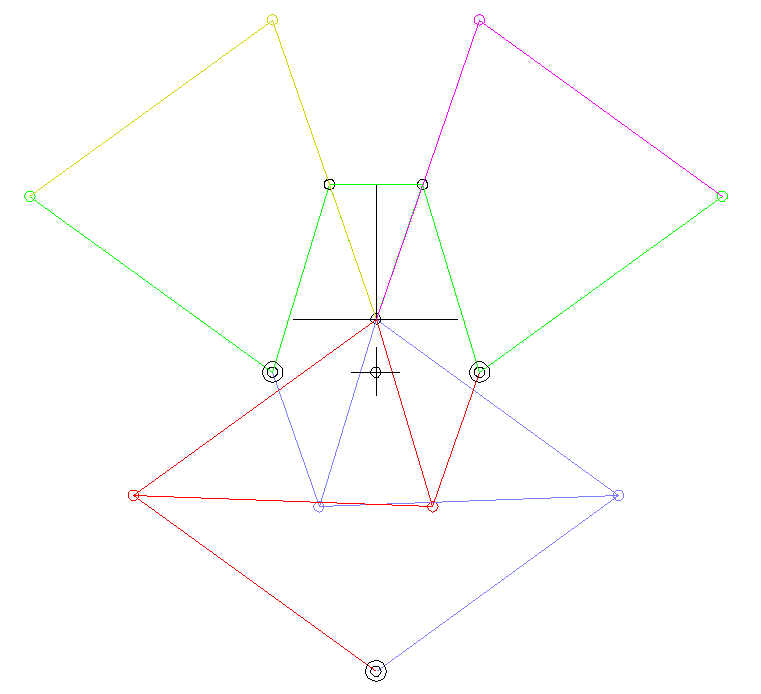
Diese Animation zeigt ein Viergelenkgetriebe mit symmetrischer Koppelkurve zur näherungsweisen Geradführung des Koppelpunkts:

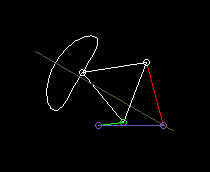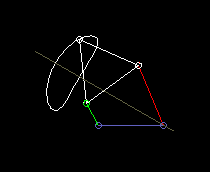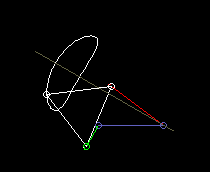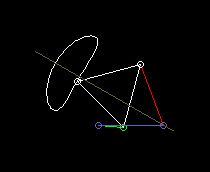
Nach dem Satz von Roberts findet man für ein Viergelenkgetriebe, das eine bestimmte Koppelkurve erzeugt, immer noch zwei ganz andere, die genau die gleiche Koppelkurve erzeugen.

Der Satz von Roberts hilft dann dabei, ein Viergelenkgetriebe für den gegebenen Bauraum oder für das richtige Antriebsglied zu finden.

zurück zum Start der Seite

Schubkurbel

Die Schubkurbel ist ein auch sehr verbreitetes viergliedriges Koppelgetriebe. Ein drehender Antriebslenker (die "Kurbel") bewegt über eine Koppel einen Abtriebsschlitten. Neben dem unbeweglichen Gestell, der Kurbel und der Koppel zählt auch der Abtriebsschlitten als Getriebeglied.

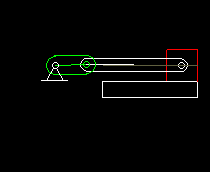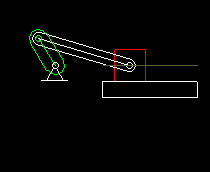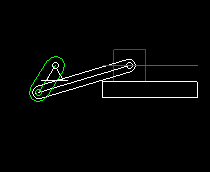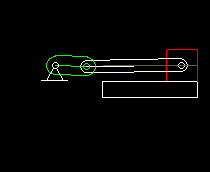
Die Schubkurbel wird vorwiegend als Übertragungsgetriebe eingesetzt, um aus einer drehenden Antriebsbewegung eine oszillierende lineare Abtriebsbewegung zu machen.

Schubkurbeln werden dabei sowohl mit Servoantrieben als auch mit Kurvengetrieben kombiniert. Diese Animation zeigt ein Kurvenscheiben-Getriebe mit Schwinghebel, bei dem eine Schubkurbel die Bewegung auf den Abtriebsschlitten überträgt.

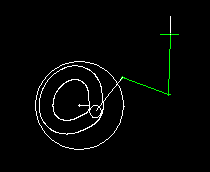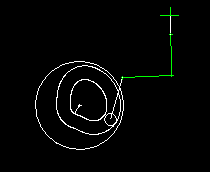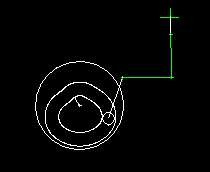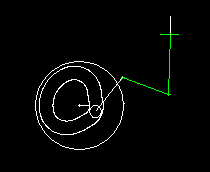
Bei der Auslegung der Servoantriebe mit Nennmoment und Spitzenmoment ist es sehr wichtig, die Nichtlinearität des Schubkurbeltriebs zu berücksichtigen, weil sonst mit völlig falschen Belastungen gerechnet wird.

In Kombination mit Servoantrieben wird am häufigsten die zentrische Schubkurbel eingesetzt, bei der die Gerade, auf der sich der Koppelendpunkt bewegt, durch den Kurbeldrehpunkt läuft:

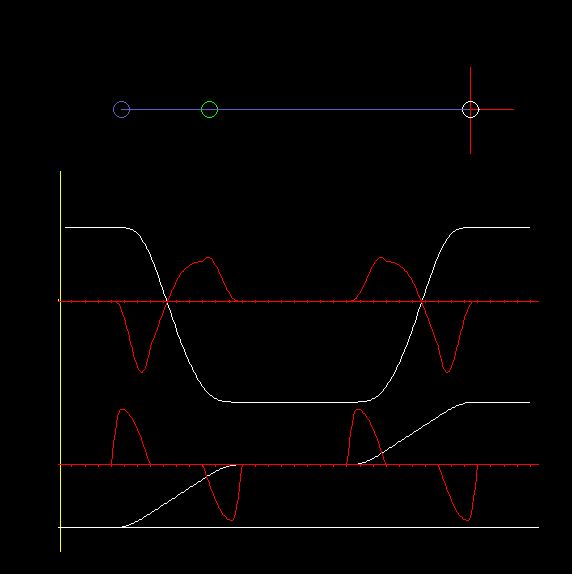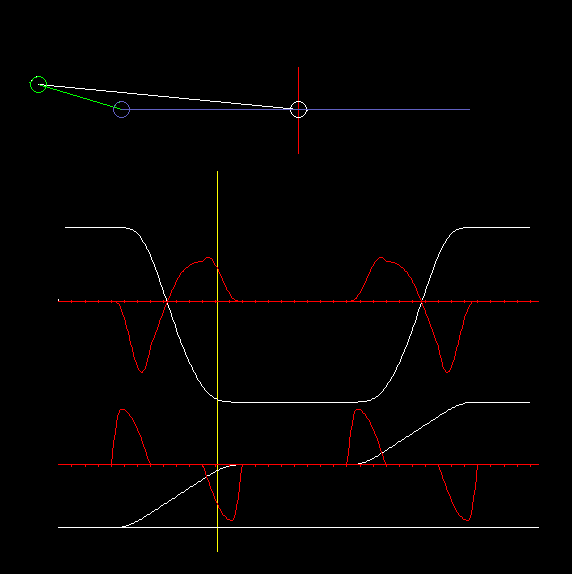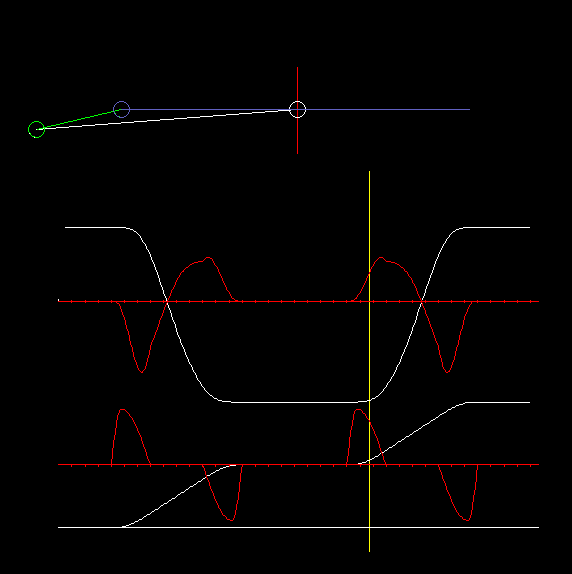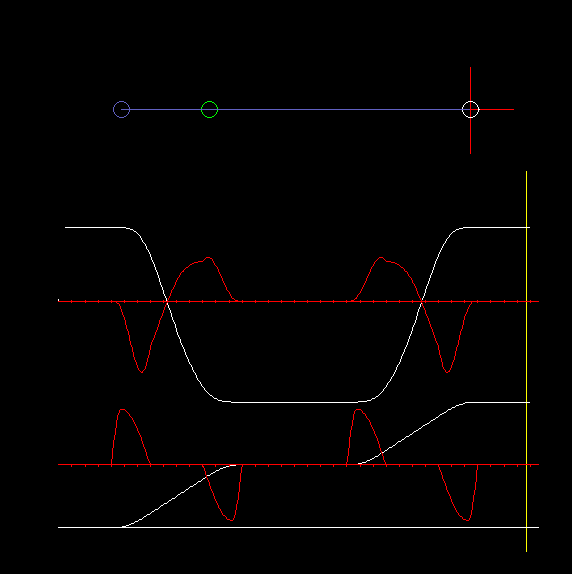
Die Animation zeigt eine zentrische Schubkurbel und Diagramme für Weg und Beschleunigung am Schlitten (oben) und am Servoantrieb (unten).

Bei der umlaufenden zentrischen Schubkurbel überstreicht die Kurbel für beide Hübe (nach links und nach rechts) jeweils 180 Grad Antriebswinkel.

Auf welcher Seite der Schubgeraden die Schubkurbel läuft, ist dabei für das Übertragungsverhalten unerheblich. Mit der gleichen Bewegungscharakteristik an der Kurbel kann die gleiche Bewegung am Abtrieb erzeugt werden, egal, ob die Kurbel mit oder gegen den Uhrzeigersinn umläuft oder "oben rum" oder "unten rum" oszilliert.

Die Schubkurbel hat Eigenschaften, die sie für die Bewegungsübertragung besonders attraktiv machen:

• Der Schlitten hält seine Endlagen auch dann sehr genau ein, wenn der Servo seine Endpositionen nur ungenau anfährt. Je näher der Mechanismus an eine Endlage (eine "Totlage") herankommt, desto weniger bewegt sich der Schlitten im Verhältnis zum Antriebswinkel.
• In den Endlagen kann man den "Kniehebeleffekt" nutzen, um mit kleinem Antriebsmoment hohe Kräfte am Abtrieb zu erzeugen. Das wird oft zum Pressen, Prägen oder Umformen ausgenutzt. Entfernt von den Endlagen können dagegen relativ große Hübe erzeugt werden. Den Kniehebeleffekt kann man verstärken, indem man zwei Kniehebel hintereinander schaltet (“Doppelkniehebel”).

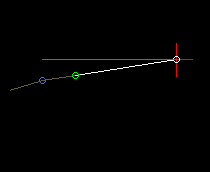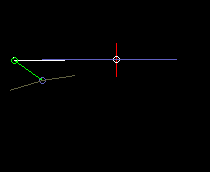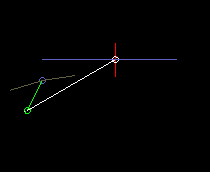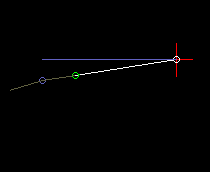
Bei der exzentrischen Schubkurbel durchläuft die Kurbel unterschiedliche Winkel für beide Hubrichtungen, d.h. die exzentrische Schubkurbel arbeitet nicht symmetrisch. Hier ist es durchaus von Bedeutung, auf welcher Seite die Schubkurbel läuft, bezogen auf die Verbindungsgerade vom Kurbeldrehpunkt zum Schlittenanlenkpunkt.

Die Animation weiter oben mit Kurvenscheibe und Abtriebsschieber ist ein Beispiel für eine Schubkurbel mit großer Exzentrizität.

zurück zum Start der Seite

Berechnung (Analyse) von Gelenkgetrieben

Mit der kinematischen "Analyse" von Koppelgetrieben ist gemeint, die Lage aller bewegten Teile zu ermitteln, nachdem Bewegungsvorgaben gemacht wurden. Dabei sind in jeder Getriebestellung so viele unabhängige Bewegungsvorgaben notwendig, wie das Koppelgetriebe Freiheitsgrade besitzt.

Für die Koppelgetriebeanalyse gibt es verschiedene alternative Ansätze, zum Beispiel:

1. Die "Zeichenfolge-Rechenmethode"

Diese Methode ist sehr alt und wurde schon verwendet, als Mechanismen noch nicht mit Computern, sondern am Reißbrett konstruiert wurden.

Bei der Zeichenfolge-Rechenmethode wird zunächst eine Getriebestellung zeichnerisch konstruiert, mit Zirkel, Lineal und Bleistift. Diese Zeichnungen bestehen schließlich aus etlichen zusammenhängenden Dreiecken. Die einzelnen Konstruktionsschritte werden dann algebraisch nachempfunden, um mit Hilfe von Cosinussatz, Sinussatz, Satz des Pythagoras und allgemein Sinus-, Cosinus- und Tangens-Funktionen sukzessive Längen und Winkel an den Dreiecken zu berechnen. Schließlich kommt man zu einer langen Folge von Berechnungsformeln, um aus den Bewegungsvorgaben die Ausgangsgrößen der kinematischen Analyse zu berechnen.

Es ist klar, dass die gesamte komplizierte Formelherleitung für jeden Mechanismus und auch für jede Art der Bewegungsvorgabe komplett neu durchgeführt werden muss.

Will man die Bewegung wechselweise am Antrieb und am Abtrieb vorgeben, so müssen zwei Formelsätze hergeleitet werden!

Die Formeln sind wegen der trigonometrischen Funktionen lang und unhandlich, und spätestens, wenn Geschwindigkeiten und Beschleunigungen berechnet werden sollen, macht das Verfahren keinen Spaß mehr.

Als Kind konnte ich in den 1970er-Jahren beobachten, wie mein Vater solche Zeichnungen am Reißbrett erstellte, dann Formeln entwickelte und diese schließlich mit seinem Diehl Alphatronic-Computer programmierte.

Noch einen wesentlichen Nachteil hat die Zeichenfolge-Rechenmethode: mit ihr können nicht alle Mechanismen berechnet werden.

Für manche Kombinationen aus Getriebestruktur und Bewegungsvorgabe können gar keine analytischen Formeln hergeleitet werden!

2. Die Modulmethode

Die Modulmethode ist eine algorithmische Weiterentwicklung der Zeichenfolge-Rechenmethode.

Bei der Zeichenfolge-Rechenmethode leitet man im Grunde oft die gleichen Zusammenhänge her, es wiederholt sich viel.  Deshalb liegt es nahe, wiederverwendbare Unterprogramme für logische Teilschritte der kinematischen Analyse zu entwickeln.

Jedes Unterprogramm entspricht einer gelenkigen Anordnung von Getriebegliedern zusammen mit definierten Ein- und Ausgangsgrößen.

Eine solche Kombination aus Getriebegliedern, Eingangsgrößen und Ausgangsgrößen wird "Modul" genannt, oder auch "Einzelglied" bzw. "Zweischlag". Die kinematische Kette, die die Kombination aus Getriebegliedern mit Gelenken ausmacht, wird auch "Elementarbaugruppe" oder "Dyade" genannt.

An dieser Stelle soll die VDI-Richtlinie 2729 erwähnt werden, die einige Getriebemodule beschreibt.

Wir selbst haben Koppelgetriebe bis ca. 1995 bevorzugt nach der Modulmethode berechnet, weil dieses analytischen Verfahren besonders schnelle und sehr exakte Berechnungen ermöglicht.

Diese Module sind in der Software immer noch verfügbar und nutzbar, wurden aber mittlerweile durch ein besseres Verfahren abgelöst.

Denn die Modulmethode hat auch gravierende Nachteile:

• Will man Bewegungen an verschiedenen Stellen des Mechanismus vorgeben, z.B. am Antrieb und am Abtrieb, müssen jeweils neue Modulfolgen definiert werden.
• Manche Mechanismen können mit der Modulmethode gar nicht berechnet werden, weil die analytische Herleitung der Berechnungsformeln nicht möglich ist. Solche Mechanismen können nur mit Iterationsverfahren berechnet werden.
• Das Zusammenstellen von Modulen für die Mechanismenberechnung ist ziemlich abstrakt und erinnert stark an das Programmieren von Software. In unseren Softwareschulungen vor 20 Jahren haben wir oft erlebt, wie schwer sich Konstrukteure mit dem Modulkonzept tun.

Ein Beispiel zeigt, wie unübersichtlich die Analyse von Koppelgetrieben mit der Modulmethode sein kann.

Die Modulmethode kann übrigens auch für die kinetostatische Berechnung der Gelenklasten in Mechanismen verwendet werden. Das ist aber sehr abstrakt und umständlich und für die Praxis ziemlich unbequem.

3. Die iterative kinematische Analyse

Heute verwenden wir in unserer Software OPTIMUS MOTUS einen für den Anwender sehr viel einfacheren und anschaulicheren Ansatz zur Modellierung von Mechanismen.

Man legt einfach nur noch grafisch fest, an welchen Elementen Getriebeglieder miteinander gekoppelt sind - fertig!

So können mit einer einzigen einfachen Funktion beliebig komplexe Mechanismenstrukturen aufgebaut werden.

Die Software erkennt die definierte Getriebestruktur automatisch und baut sich den Berechnungsgang für die kinematische und kinetostatische Analyse selbstständig zusammen, immer ausgehend von den definierten Bewegungsvorgaben.

Wenn die Bewegungsvorgaben zwischen Antrieb und Abtrieb wechseln, braucht der Anwender am Mechanismenmodell gar nichts zu ändern. Der Strukturerkennungsalgorithmus organisiert automatisch einen neuen Berechnungsgang.

Spezielle Optimierer sorgen dafür, dass die kinematische Analyse fast genauso schnell abläuft wie bei der Modulmethode.

Die Berechnung selbst basiert auf nichtlinearen Gleichungssystemen, die aus Zwangsbedingungen zusammengestellt werden und jeweils so komplex sind, wie es die definierte Getriebestruktur erfordert. Wo es möglich ist, verwendet der Berechnungsalgorithmus intern auch analytische Berechnungsfunktionen. Auch das organisiert der Algorithmus aber automatisch, der Anwender braucht nichts dafür zu tun.

zurück zum Start der Seite

Kurven-Koppelgetriebe

Sehr häufig werden Koppelgetriebe zum Übertragen von Bewegungen von einer Kurve auf ein Werkzeug verwendet.

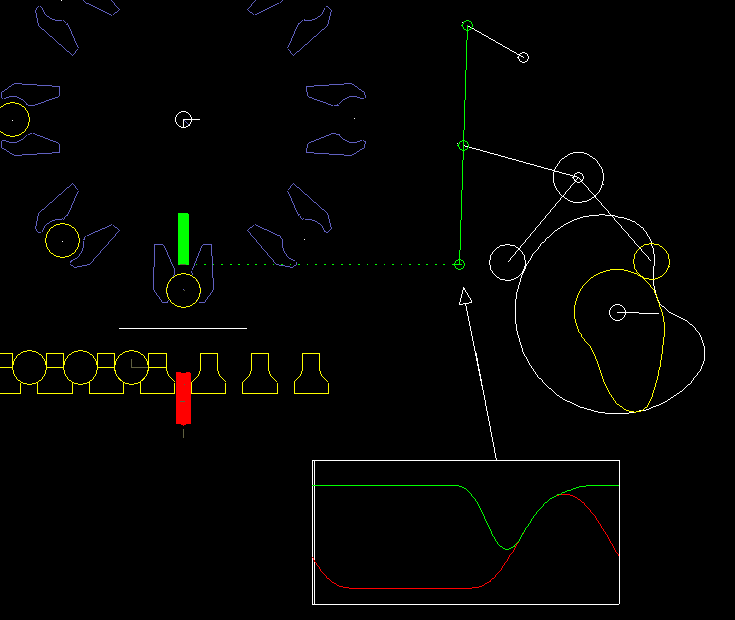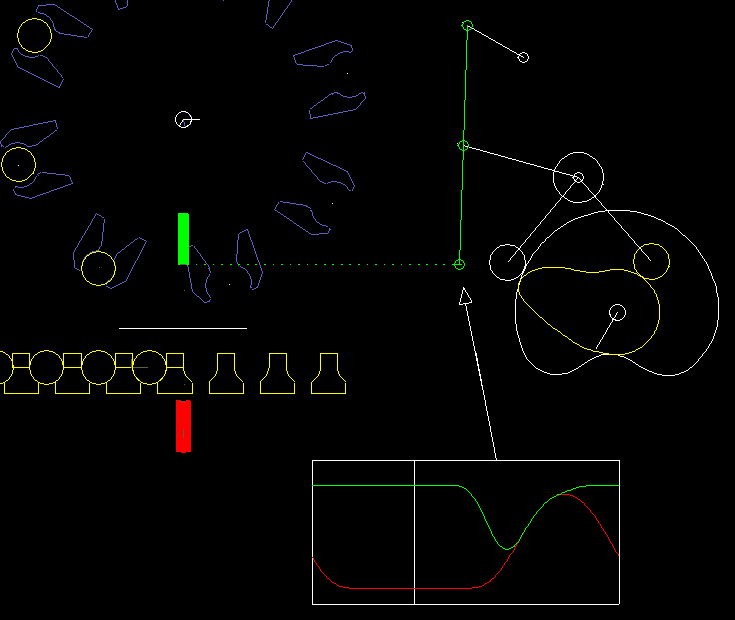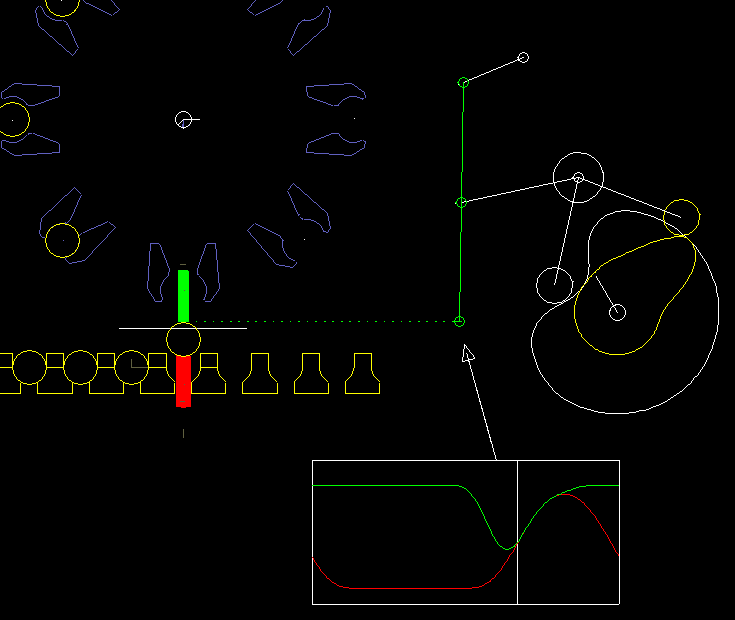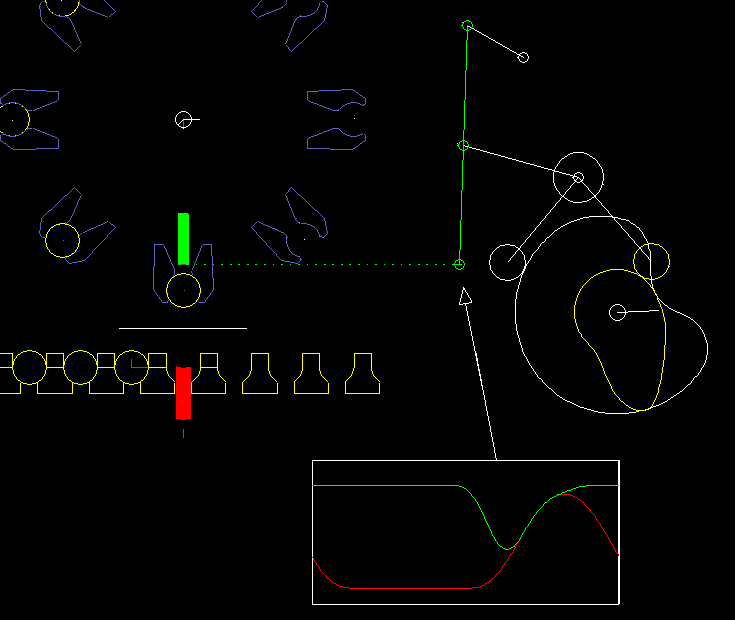
Hier ein Beispiel aus einer Verpackungsmaschine:

Ein Unterstempel (rot) und ein Oberstempel (grün) heben gemeinsam einen Artikel (z.B. eine Brausetablette) aus einer Kette und nehmen gleichzeitig ein Papier (weiße Linie) mit, das zwischen Oberstempel und Artikel eingeklemmt wird. Artikel und Papier werden in einen Greifer auf einem Faltkopf (blau) eingeschoben. Um Artikel und Papier sicher und schonend zu bewegen, müssen Oberstempel und Unterstempel phasenweise ziemlich synchron laufen. Optimal ist: ganz synchron.

Rechts ist das Kurven-Koppelgetriebe für den Oberstempel dargestellt.

Das Koppelgetriebe wurde durch Koppelgetriebesynthese so optimiert, dass der Greifpunkt am Oberstempel möglichst genau geradlinig läuft.
Die Vertikalbewegung wird am Greifpunkt exakt synchron zum Unterstempel vorgegeben.

Mit iterativer kinematischer Analyse wird die entsprechende Bewegung der Rollen berechnet und damit die Kurvenbahnen.

Bemerkenswert ist hier, dass der Greifpunkt und damit der Angriffspunkt für die Bewegungsvorgabe auf der Koppel eines viergliedrigen Getriebes liegt. Obwohl diese Getriebestruktur recht einfach aussieht, ist weder die Zeichenfolge-Rechenmethode direkt darauf anwendbar, noch läßt sich die Struktur in Einzelglieder und Zweischläge zerlegen. In der Software OPTIMUS MOTUS braucht man sich um diesen Umstand gar nicht zu kümmern.

zurück zum Start der Seite

Koppelgetriebesynthese

Bei der Synthese sucht man Koppelgetriebe mit bestimmten Eigenschaften.

Diesem relativ komplizierten Thema haben wir eine eigene Seite “Getriebesynthese” gewidmet.

zurück zum Start der Seite

Verzweigungslagen

Mechanismen können Verzeigungslagen bzw. Totlagen erreichen, aus denen zwei Wege heraus führen.

Ein einfaches Beispiel ist die Schubkurbel. Erreicht sie die Strecklage (Kurbel und Koppel verlängern sich gegenseitig) oder die Decklage (Kurbel und Koppel überdecken sich), so kann die Kurbel sowohl im Uhrzeigersinn als auch im Gegenuhrzeigersinn weiterbewegt werden.

Bei der Modulmethode werden binäre Parameter (K=+1 oder K=-1) definiert, um die gewünschte Getriebelage zu wählen.

Bei der iterativen Analyse kann die gewünschte Bewegungsfortsetzung ähnlich einfach ausgewählt werden.

zurück zum Start der Seite

Modulbibliothek

Mit den Kinematik- und Kinetostatik-Modulen steht eine umfangreiche Bibliothek an Berechnungsfunktionen für kinematische Strukturen zur Verfügung.

Diese Bibliothek kann nicht nur innerhalb der Mechanismensoftware OPTIMUS MOTUS eingesetzt werden, sondern auch in C- und ST-Quelltexten (strukturierter Text) innerhalb von SPS-Projekten.

Sprechen Sie uns an!

zurück zum Start der Seite

zur Startseite Nolte NC-Kurventechnik GmbH

Start Fachberichte Mechanismen Kinematik Kurvengetriebe Schrittgetriebe Servo/SPS Bewegungsdesign Fortbildung Service Kurvenberechnung Software Impressum Datenschutz
Viergelenk Schubkurbel Analyse Kurven-Koppelgetriebe Synthese Verzweigungslagen Modulbibliothek

> zu unseren Kontaktdaten