Kollisionsoptimierung

Kollisionsoptimierung ist die effektivste Methode, um komplexe Bewegungsteuerungen mit Kurvengetrieben und Servoachsen systematisch auf hohe Performance zu bringen. Mit Kollisionsoptimierung holt man konsequent mehr Durchsatz aus der Mechanik heraus (oft mehr als 40 %), ohne die Maschine teurer zu machen.

Nolte NC-Kurventechnik hat sich seit 1973 auf die Auslegung und Simulation der Bewegungsabläufe in komplexen Anlagen mit Kurven, Koppelgetrieben und  Servoantrieben spezialisiert und bietet (neben entsprechender Software) Kollisionsoptimierung als Dienstleistung zum Festpreis an. Zum Lieferumfang gehören DXF-Dateien der Kurvenbahnen und der Getriebenullstellung, NC-Programme zum Herstellen der Kurven sowie Diagramme, Schaubilder, Tabellen und Animationen

Der Begriff "Kollisionsoptimierung" setzt sich aus "Bewegungsoptimierung" und "Kollisionskontrolle" zusammen.

Das Prinzip ist einfach:
Man optimiert das Gesamt-Bewegungsdiagramm und simuliert gleichzeitig den Bewegungsablauf grafisch.
Man versucht, die Kollisionen in der Bewegungssimulation knapp zu vermeiden und dabei die dynamischen Belastungen gleichmäßig auf alle Einzelantriebe und über die Zeit zu verteilen und so zu minimieren. Letztlich sollen alle Einzelantriebe theoretisch die gleiche, möglichst hohe Taktzahl erreichen. Dabei kann man sich Schritt für Schritt immer die kritischste Stelle der Bewegungsauslegung vornehmen und entschärfen, bis man keinen Ansatz mehr für eine Verbesserung findet.

In der Praxis ist dieses iterative Vorgehen recht intuitiv umsetzbar, obwohl einiges dahinter steckt, denn es sind etliche Bewertungskriterien zu berücksichtigen. Die Simulationen und die Diagramme für Beschleunigungen, Kräfte, Momente, Pressungen usw. weisen aber von sich aus den Weg, wenn man nur hinschaut.

Je mehr Erfahrung man mit der Methode hat, desto weniger Iterationsschritte benötigt man.

Wichtig ist jedoch das richtige Werkzeug für die Kollisionsoptimierung. Es muss Simulationen und Bewertungen schnell, innerhalb von Sekunden, aktualisieren. Unsere Software OPTIMUS MOTUS ist dafür hervorragend geeignet. Sie ist genau für solche Optimierungen entwickelt worden.

Direkt zu ...

• weiter im Text
• Das richtige Werkzeug
• Beispiel Sammelscheibe
• Beispiel Biegeautomat
• Beispiel Buchstapler
• Beispiel Durchlaufteile für Kaugummi-Einzelpack
• Beispiel Faltwerkzeuge
• Beispiel Etikettenbeleimung
• ausführliches Pick&Place-Beispiel mit Protokoll der Performance-Steigerung
• Berechnung

zur Startseite von Nolte NC-Kurventechnik GmbH

> English version of this page

Beispiel Sammelscheibe

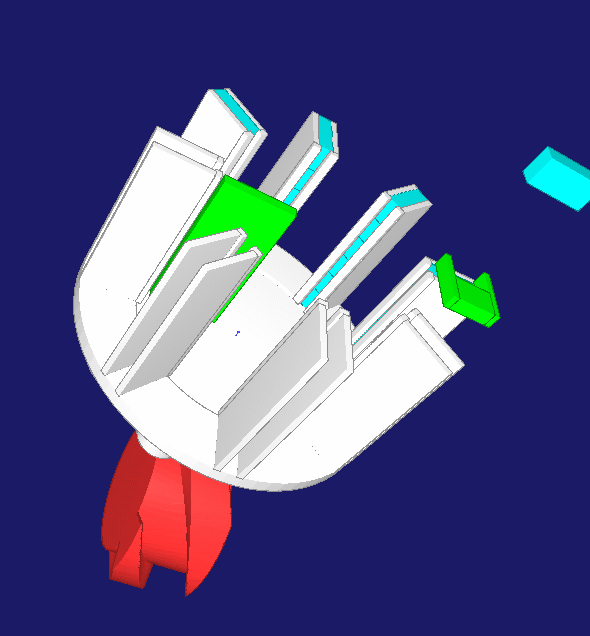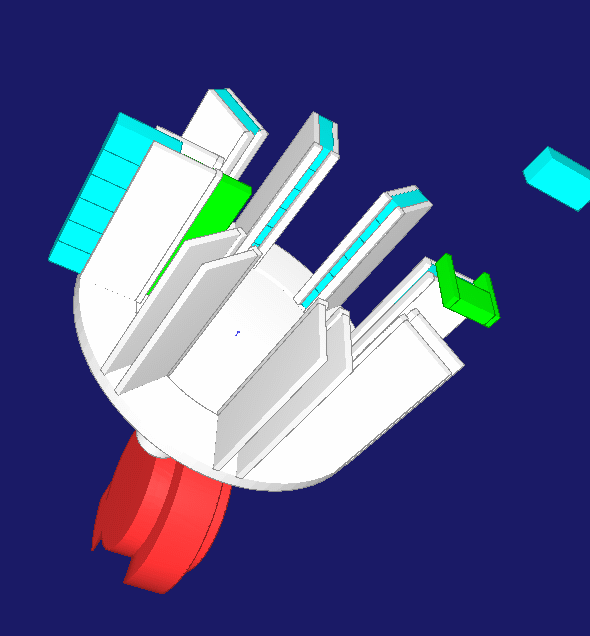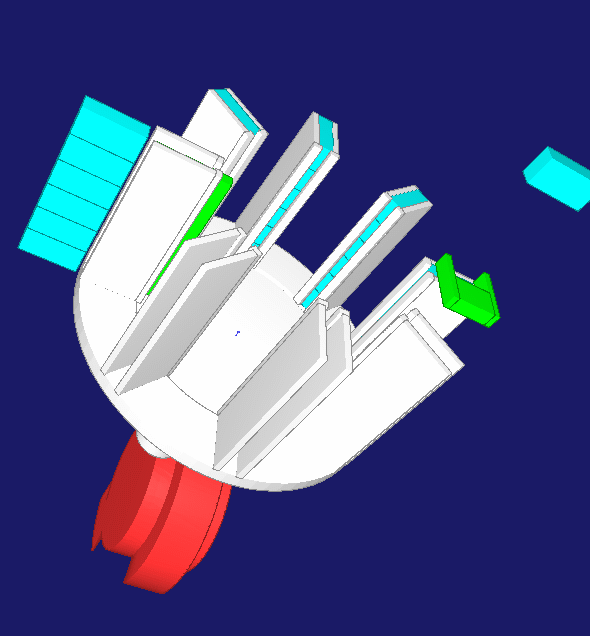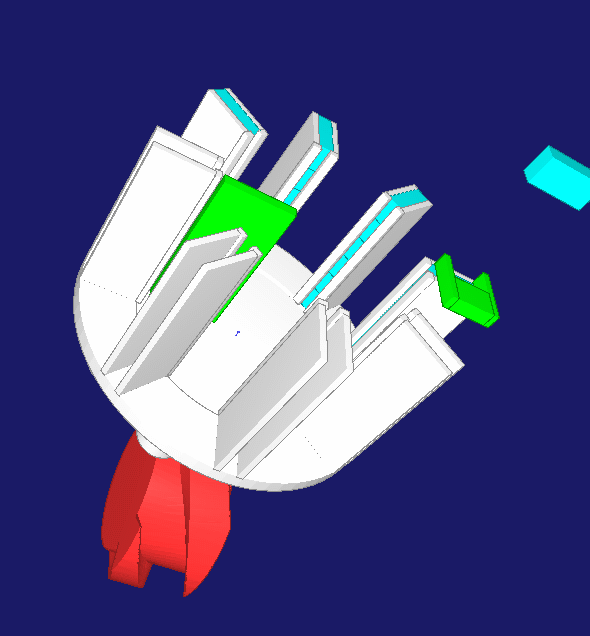
Ein Rechen sammelt 3 bis 8 Einzelartikel in einer Sammelscheibe, bis eine Artikelreihe vollständig ist. Dann taktet die Sammelscheibe eine Teilung weiter. Nach 180 Grad Drehung wird die Artikelreihe in die Sammelpackmaschine ausgeschoben. Für die getaktete Drehung der Sammelscheibe bleibt nur die sehr kurze Zeit zwischen zwei Einzelartikeln, im praktischen Anwendungsfall ca. 25 ms. Um diese Schaltzeit bei variabler Anzahl Einzelartikel mit einem kompakten Mechanismus zu erreichen, wird ein Servoantrieb mit einem Zylinderkurven-Schrittgetriebe kombiniert. Auf ein Trigger-Signal hin beschleunigt der Servo die mechanische Kurve auf Maximaldrehzahl, ohne dass die Sammelscheibe sich dreht. Während einer Schaltphase bei konstanter Kurvendrehzahl dreht die Sammelscheibe um eine Teilung weiter. Anschließend bremst der Servo ohne Drehung der Sammelscheibe ab bis in den Stillstand nach 360 Grad Drehwinkel. Die Trägheiten von Servomotor+Zylinderkurve und Sammelscheibe+Artikel bewirken nicht gleichzeitig ein Antriebsmoment, so dass das Maximalmoment sinkt. Der Servo hat in der Rastphase der Sammelscheibe genug Zeit, die Kurve auf Drehzahl zu bringen. Die Zylinderkurve kann klein gehalten werden, weil sie über einen großen Anteil des Gesamtzyklus einer Sammelpackung stillsteht.
Die gesamten Bewegungen wurden mit OPTIMUS MOTUS (R) so aufeinander abgestimmt, dass Maximal- und Effektivmoment am Servo minimal und damit die Taktzahl maximal werden. Dabei wurden auch der erforderliche Kurvendrehwinkel für die Schaltung, die Kurvenbreite und der Kurvendurchmesser optimiert, die Zylinderkurve neu berechnet und das resultierende Eigenträgheitsmoment der Zylinderkurve berücksichtigt.

Beispiel Bihler-Biegemaschine

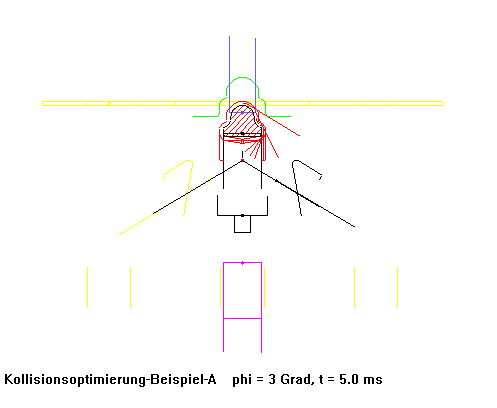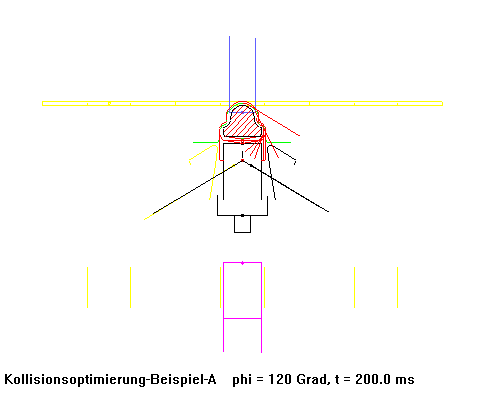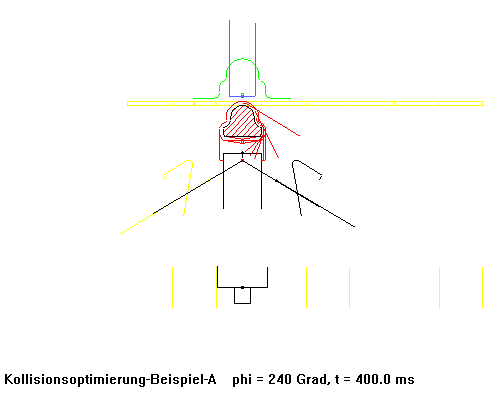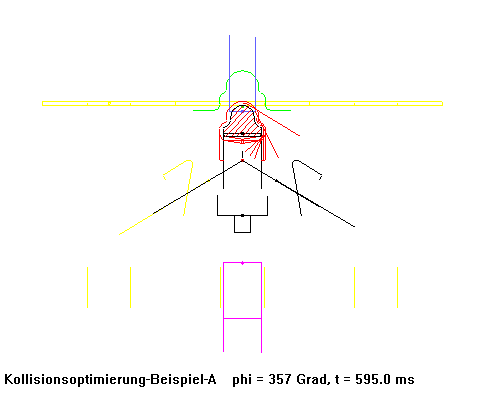
Eine Biegemaschine produzierte mit  herkömmlich berechneten und NC-gefrästen Kurven Rohrschellen anfangs mit 70 Takten pro Minute. Nachdem die Kurven in dieser Maschine durch einen  kollisionsoptimierten Kurvensatz ersetzt wurden, produzierte sie schließlich mit 250 (!) Takten pro Minute bei noch verbesserter Laufruhe.

Beispiel Buchstapler

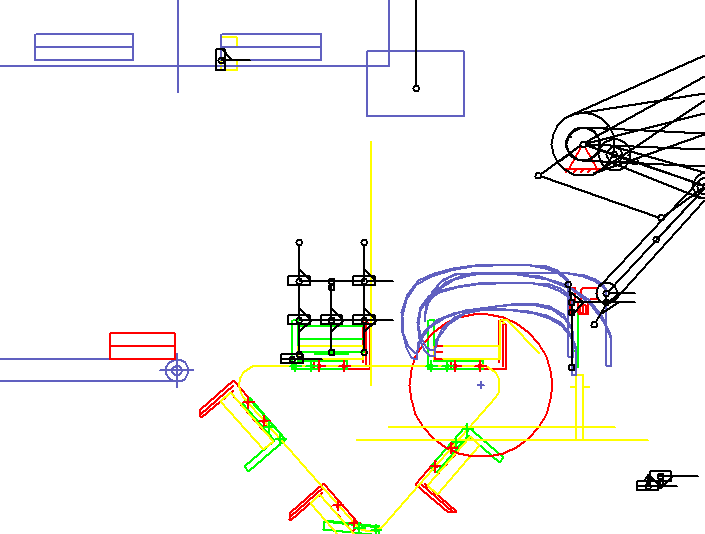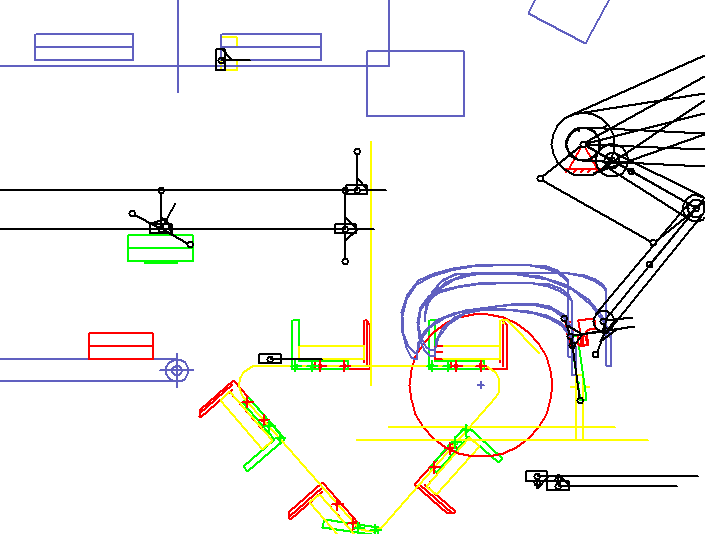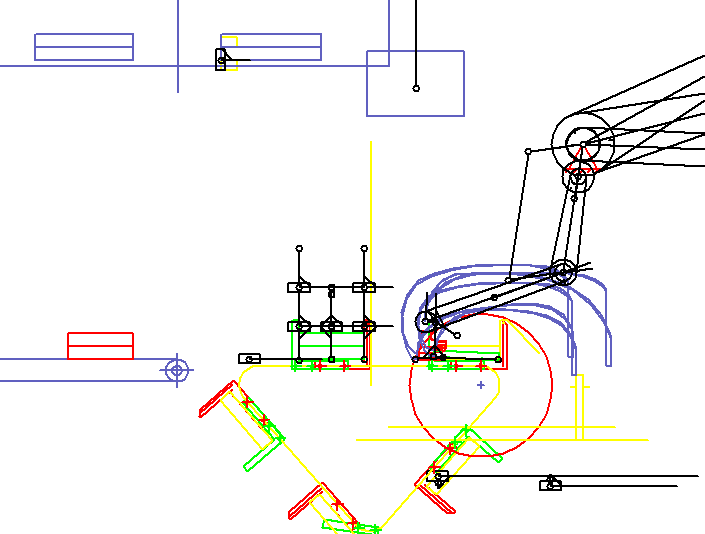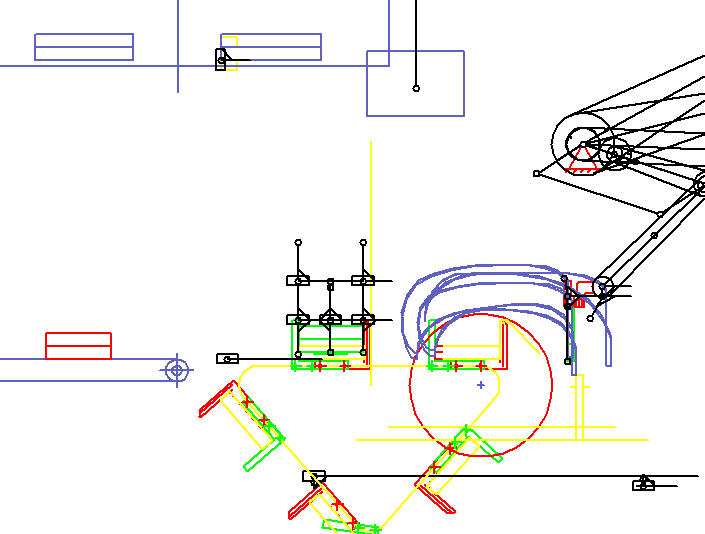
Ein Paar von Greifarmen synchronisiert sich auf einen Buchstrom auf, greift zwei Bücher, zieht sie nach oben und bremst ab und legt sie in Transportfächen auf jeweils einer Kette ab. Wenn in der Animation die XZ-Ebene sichtbar ist, so bewegt sich der Buchstrom in Y-Richtung. Die Animation zeigt nur einen der Greifarme. Der zweite ist in der Tiefe (in Y-Richtung) versetzt angeordnet.
In der Animation sind der Buchtransport und die Mitbewegung der Greifer rechts unten nur skizzenartig durch Rechtecke und Linien mit variabler Länge dargestellt. Es soll nur erkennbar sein, dass Buch und Greifer synchron fahren bzw. welche Wegdifferenz sich ergibt, wenn die Synchronität nicht genau eingehalten wird.
Im Transportfach werden mehrere Bücher gesammelt, und ein Greifer muss jeweils unterschiedliche Ablagepositionen anfahren. Insgesamt müssen die durchaus flexiblen Bücher ohne Knicke, Riefen oder ähnliche Verletzungen abgelegt werden.
Ist im Transportfach eine bestimmte Anzahl an Büchern gesammelt, wird das Transportfach weitergetaktet.
Als Option der Anlage werden die Stapel im weitergetakteten Transportfach von einer Drehstation angehoben, gedreht und auf den jeweils ankommenden Teilstapel wieder abgelegt, während die Transportfächer weitertakten. Im Transportfach vor dem Abgabeband (links) sammeln sich so mehrere Teilstapel. Die Drehstation ist links oben in zwei Ansichten dargestellt: oben das Drehen, darunter das Ablegen. Nach einer festgelegten Anzahl von Teilstapeln legt die Drehstation den Gesamtstapel auf einem langsam und gleichmäßig laufenden Abgabeband ab.

Die Anlage enthält 10 Servoantriebe mit elektronischen Kurven, und die Formatvielfalt ist riesig. Wir haben für eine solche Anlage ein parametrisches Modell erstellt, das für alle Formatvarianten eigene Bewegungsdiagramme erzeugt, inklusive Kollisionskontrolle, damit die Anlage jedes Format mit maximal möglicher Taktzahl verarbeiten kann.

Für solche Anwendungen entwickeln wir Quelltexte bzw. Funktionsbausteine für die SPS-Programmierer.

Beispiel Kaugummiverpackung (Durchlaufteile)

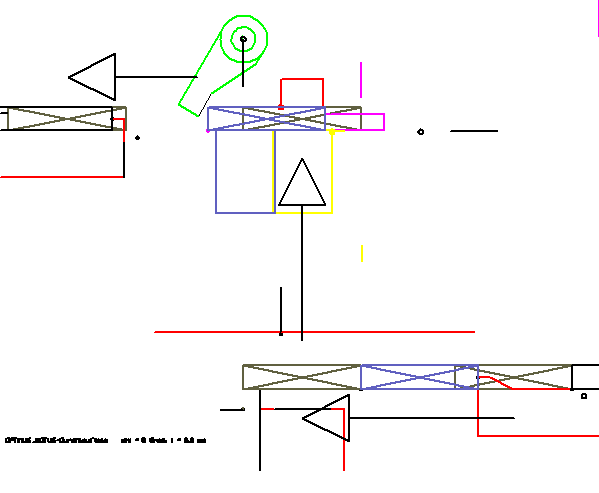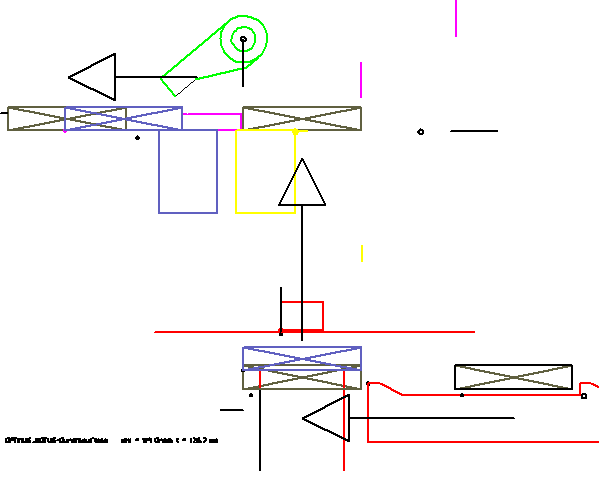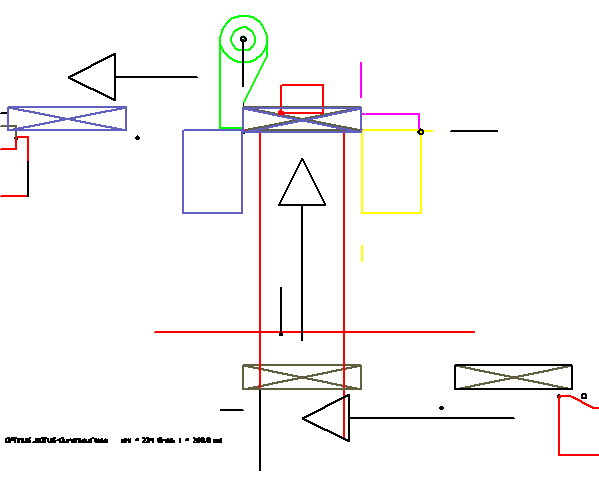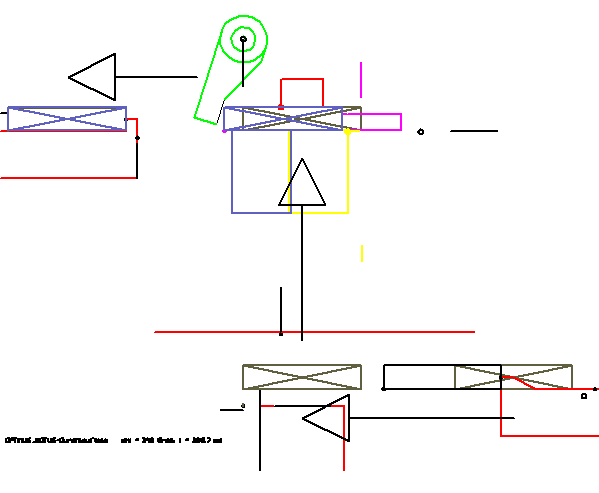
In dieser Animation sind die bewegten Teile jeweils nur durch wenige Linien skizziert. Solch eine Simulation kann quasi ad hoc erstellt werden, ohne Modellierung im CAD-System. Eine Besonderheit an dieser Animation ist die Art, wie die Bewegung des Kaugummis (Rechteck mit Kreuz) dargestellt wird. Es wird von Werkzeug zu Werkzeug weitergereicht. So wird der Durchlauf des Artikels durch die Station besonders anschaulich. In der Software OPTIMUS MOTUS steht dafür ein spezielles Feature zur Verfügung, die "Durchlaufteile".

Faltwerkzeuge

Hier werden Faltvorgänge dargestellt, um Karamellen im Durchlaufbetrieb in Papier bzw. Folie einzupacken. Speziell ist die Kameraposition. Sie fährt synchron zum Artikel mit. Die gegenseitigen Abhängigkeiten der Einzelbewegungen sind bei dieser Anwendung besonders kompliziert. Dafür ist die Taktzahl mit >1000/min ziemlich hoch.

Beispiel Etikettbeleimung

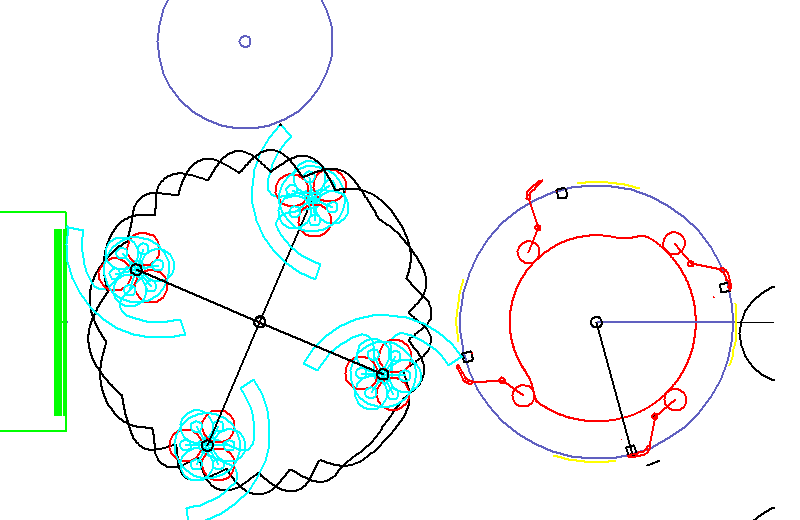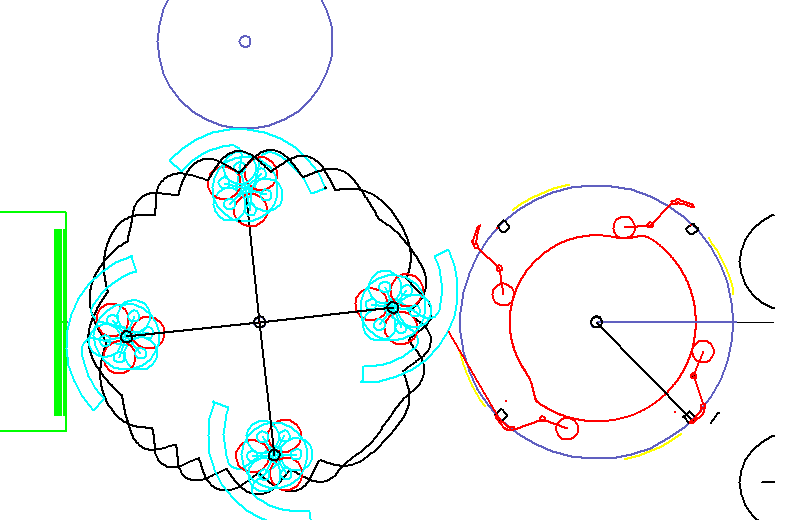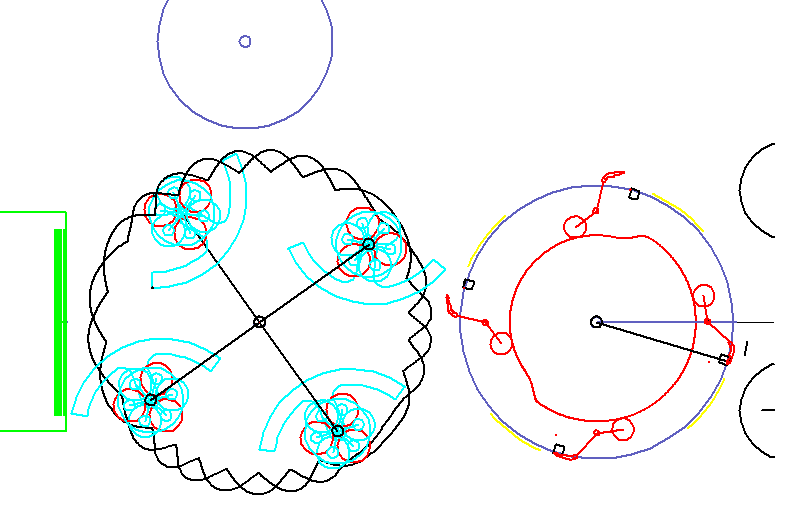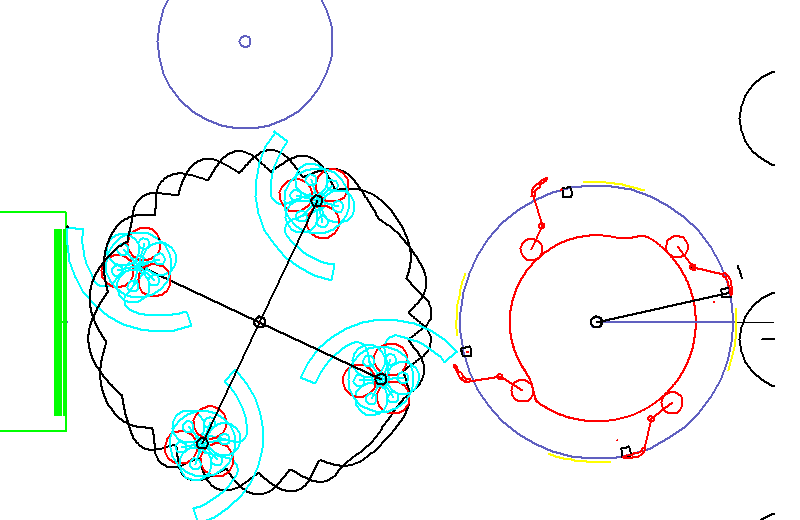
Die Animation zeigt eine Kaltleimetikettierung. Etiketten werden mit Leimsegmenten beleimt, aus einem Magazin gezogen und schließlich mit Greifern abgezogen, um auf Flaschen aufgebracht zu werden.

zum Start der Seite

Spezielleres zur Kollisionsoptimierung

Die grafischen Simulationen können 3D-Simulationen sein wie bei der Sammelscheibe oder 2D-Animationen wie bei Buchstapler, Kaugummi-Einzelpack, Faltung oder Beleimung.

3D ist cooler, aber 2D ist für Kollisionskontrollen praktischer, weil man Überschneidungen von Teilen sofort sieht. Im 2D muss man nicht erst die richtige Perspektive finden, um zwischen Freigängigkeit und Kollision unterscheiden zu können. 2D-Animationen können grafisch so organisiert werden, dass mehrere Kollisionsstellen nahe beieinander dargestellt werden und man für die Überwachung nicht zwischen Ansichten springen muss. Diese Darstellungen entsprechen 2D-Zeichnungen mit mehreren Ansichten und Detailansichten.

Die Kinematik-Simulationen können natürlich die komplette detaillierte Geometrie aller bewegten und unbewegten Teile inklusive Schrauben, Federn, Energieketten, Kabeln usw. enthalten, aber das ist beileibe nicht erforderlich. Wenn die Animationen nicht gleichzeitig jemanden beeindrucken sollen, reicht es, nur die Geometrie darzustellen, für die Kollisionsgefahr besteht. Das sind mitunter nur ein paar Linien oder Kreisbögen.

Kollisionsoptimierung ist erheblich wirkungsvoller, als nur "das richtige" Bewegungsgesetz auszusuchen.

Durch bloßes Austauschen von Bewegungsgesetzen läßt sich die erreichbare Taktzahl nur wenig beeinflussen (realistisch meist ca. 5 %).
Mit der Kollisionsoptimierung haben wir die Taktzahl sehr häufig um 40 % oder mehr gesteigert, bei einzelnen Anwendungen sogar um 250 %!

Die Taktzahl der Gesamtanlage wird letztlich immer durch eine dynamische Grenze bei einer kritischen Achse begrenzt.
Bei der Kollisionsoptimierung werden die Bewegungsabläufe unter Berücksichtigung aller dynamischen Grenzen (

• Bewegungsbereiche,
• Geschwindigkeit,
• Beschleunigung,
• Ruckfunktion,
• Kraft,
• Maximalmoment,
• Nennmoment,
• Pressung,
• Zugfestigkeit,
• Mindestlebensdauer,
• Schwingungsanregung

usw.) für alle Kurven und Servoantriebe umfassend so gestaltet, dass die Gesamtanlage eine möglichst hohe Taktzahl erreichen kann. Dabei wird die dynamische Last gleichmäßig über alle Bewegungsachsen und auch über die Zeit verteilt. Alle Bewegungsachsen (Kurven, Servoantriebe usw.) sollten gleich intensiv ausgelastet sein. Stärker belastete Achsen und Bewegungsphasen werden entlastet, während Achsen und Bewegungsphasen mit dynamischer Reserve mehr zugemutet wird.
Dieser Lastenausgleich ist quasi ein "sozialer Gedanke" für das Miteinander der Bewegungsachsen.
Im Betrieb mit einer vorher festgelegten Nenntaktzahl erreicht man so eine möglichst große dynamische Reserve und geringen Verschleiß.

Für jedes dynamische Kriterium und jede Bewegungsachse kann man abschätzen, welche Taktzahl theoretisch erreichbar ist.

Beispiel:
Eine Servoachse bewegt eine Masse nach einem bestimmten Bewegungsverlauf hin und her. Andere Belastungen als Massenträgheit sind nicht relevant. Der Motor kann 9 Nm aufbringen. Bei 100 Takten/min wird ein maximales erforderliches Antriebsmoment von 4 Nm berechnet.
Da das aus Trägheit entstehende Antriebsmoment quadratisch mit der Taktzahl steigt, kann die Taktzahl um den Faktor 1,5 erhöht werden, denn 1,5² = 9 Nm / 4 Nm. Theoretisch könnte die Achse also bis 150 Takten/min betrieben werden, bevor das Antriebsmoment zu groß wird.

Ähnliche Abschätzungen lassen sich für alle dynamischen Kriterien und alle Achsen anstellen. Ziel der Kollisionsoptimierung ist, die kleinste so abgeschätzte Taktzahl möglichst groß werden zu lassen. In der Praxis führt man diese Abschätzungen aber nicht unbedingt explizit aus. Statt dessen prüft man einfach, welche dynamische Belastung im Verhältnis zum entsprechenden Grenzwert besonders groß ist, und entschärft diese Stelle.

Sie können die Gesamtoptimierung auch so angehen:

Sie setzen für die Bewertung der Bewegungsauslegung zunächst eine bestimmte Taktzahl fest und optimieren alle Bewegungen durch Bewegungsdesign, um diese Taktzahl einzuhalten.
Wenn das nicht möglich ist, verringern Sie die Taktzahl etwas und optimieren neu.
Wenn es doch möglich ist, vergrößern Sie die Taktzahl und optimieren ebenfalls neu!

Mit dieser Iteration finden Sie schließlich auch heraus, welche Taktzahl die Anlage rechnerisch erreichen kann.

Das klingt kompliziert, ist in der Praxis aber ein ganz intuitiver Vorgang. Mit Erfahrung geht es aber etwas schneller.

"Optimieren" bedeutet auch, den kritischen Bewegungsabschnitten auf den Achsen mehr Zeit zu geben. Diese Zeit muss man anderen Achsen und Bewegungsabschnitten wegnehmen, sonst würden sich Bewegungen zeitlich so überschneiden, dass die bewegten Teile kollidieren. In den Bewegungssimulationen sieht man die Kollisionen dann unmittelbar.

zum Start der Seite

Das richtige Werkzeug für die Kollisionsoptimierung

Kollisionsoptimierung ist systematisches und konsequentes Bewegungsdesign für die Maschine unter Berücksichtigung vielfältiger dynamischer Bewertungskriterien.

Kollisionsoptimierung macht nur Spaß, wenn die einzelnen Iterationsschritte schnell ausgeführt werden können, denn sonst wäre das Verfahren nicht mehr intuitiv anwendbar. Als Nutzer muss man schnell erkennen und lernen, welche Auswirkungen bestimmte Änderungen an der Bewegungsgestaltung haben.

Ohne Software läuft da nichts, und die Software muss folgendes bieten:

• interaktives Bewegungsdesign mit vielfältigen Möglichkeiten, Bewegungsgesetze und Bewegungen zu gestalten (für die dynamische Qualität der Bewegungen)
• grafische Simulationen (für die Kollisionskontrolle)
• kurze Rechenzeiten für die Simulationen (wenige Sekunden)
• schnelle Bereitstellung aktueller Werte für alle Bewertungskriterien

Speziell für diese Anforderungen haben wir die Software OPTIMUS MOTUS entwickelt.
Wir und viele andere Anwender setzen sie seit Jahrzehnten mit großem Erfolg für die dynamische Optimierung komplexer Bewegungssteuerungen ein.

Kollisionsoptimierung ist Bewegungsplanung und wirkt wie eine Landkarte oder ein Navigationssystem beim Autofahren.

Wenn man Bewegungen erst in der Werkhalle und an der Maschinensteuerung gestaltet, z.B. mit den heute verbreiteten Funktionen zum Verschieben von Stützpunkten im Cam Editor, und an der laufenden Maschine testet, hat man praktisch keine Übersicht über die Auslastungsgrade der einzelnen Bewertungskriterien. Außerdem ist es riskant, sich mit der laufenden Maschine in kollisionsnahe Bereiche vorzutasten, also lässt man davon lieber die Finger und verzichtet auf Performance.

Grafische Simulationen werden vielfach in der Praxis direkt im CAD-System erstellt, wenn dort ein Kinematikmodul installiert ist, oder in einem MKS-Programm (Mehrkörpersimulation). Das funktioniert, hat aber im Rahmen der Kollisionsoptimierung Nachteile:

• Die Modellierung der erforderlichen Geometrie ist relativ aufwändig.
• Berechnungen und Simulationen laufen langsam ab.
• Es fehlt in der Regel ein leistungsfähiges Werkzeug zum Bewegungsdesign.

Zeitabhängige Bewegungen können in diesen Systemen oft nur über Kurvenbahn-Splines eingebracht werden. Dann muss behelfsweise eine Dummy-Kurve berechnet und in das Modell eingebunden werden, um den Bewegungsablauf überhaupt simulieren zu können. Dieser Behelf ist umständlich, wenn man die Kurve im Rahmen der Kollisionsoptimierung häufig ändern will.

In OPTIMUS MOTUS kann man Bewegungen an beliebiger Stelle direkt durch ein Bewegungsdiagramm vorgeben, ohne Umweg über Behelfssplines.

Software für MKS (Mehrkörpersimulation) ist sehr leistungsfähig im Hinblick auf die Modelltiefe, die Detailtreue. Die Berechnungszeiten sind aber dadurch auch erheblich größer, und die Modellkomplexität ist schwieriger zu handhaben.

Kollisionsoptimierung mit OPTIMUS MOTUS bietet das beste Verhältnis zwischen Optimierungsaufwand und Steigerung der Maschinenperformance.

zum Start der Seite

Beispiel Pick-and-Place-Anwendung

2D Pick&Place-Anwendung (PnP)

An Hand eines einfachen Beispiels mit nur 2 Bewegungsachsen wollen wir durchspielen, welche Performance-Steigerungen sich mit verschiedenen Optimierungstechniken ergeben. In "echten" Aufgabenstellungen sind oft erheblich mehr Bewegungen gegeneinander zu optimieren (typischerweise 4-10, manchmal auch mehr als 40).

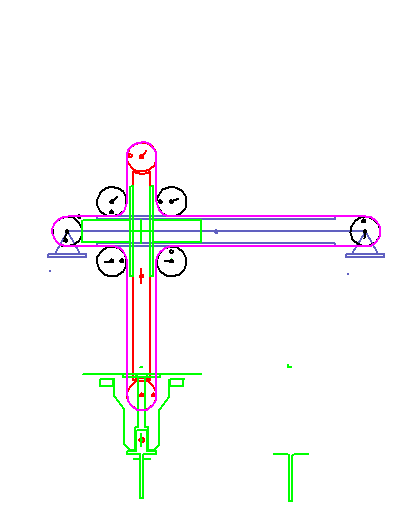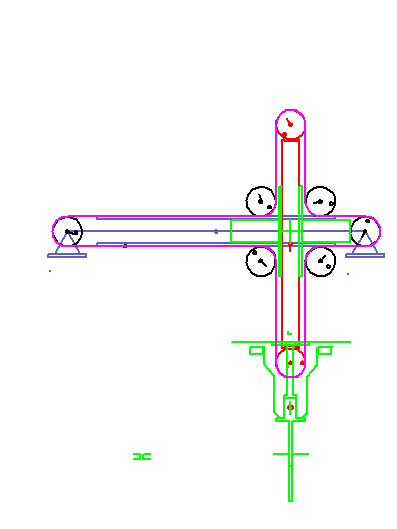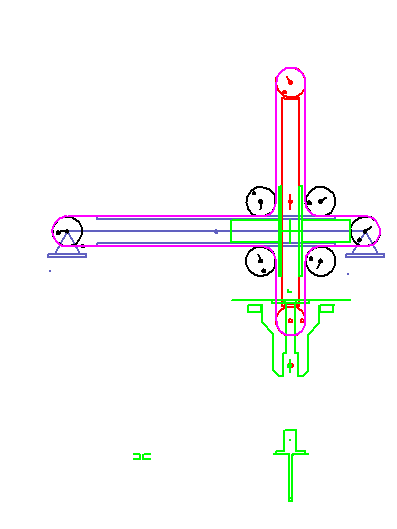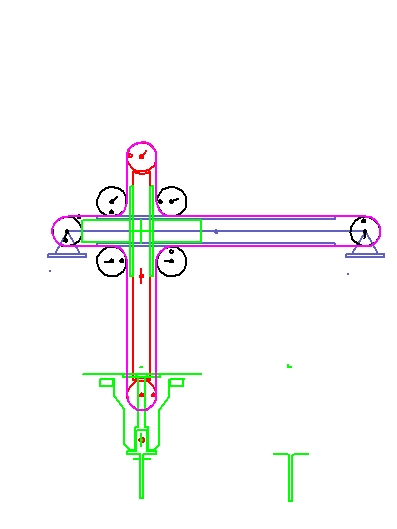
Eine Servo-gesteuerte Montageeinheit zieht Stifte aus einem Magazin und setzt sie in eine Baugruppe ein.

Die Stifte stecken 30 mm tief im Magazin und sollen auch 30 mm tief in die Baugruppe eingesteckt werden.
Abnahme- und Montagestelle liegen horizontal (X) 100 mm auseinander, vertikal (Y) auf gleicher Höhe.
Der Vertikalweg des Greifers soll 50 mm nicht überschreiten.
Der Greifer greift auf einer Länge von 10 mm und öffnet dabei 2 mm (1 mm auf jeder Seite).
Für die Öffnungsbewegung werden 40 Grad Taktwinkel benötigt.
Die Bewegungscharakteristik der Öffnungs- und Schließbewegung ist nicht genau bekannt.

Alle Bewegungen sollen ruckfrei sein, also ohne Sprünge in Weg, Geschwindigkeit und Beschleunigung.
100 Takte/min werden angestrebt.

Der Übersicht halber werden beide Bewegungsachsen nur mit der Maximalbeschleunigung bewertet.
Dabei sollen die Beschleunigungen in Horizontal- und Vertikalrichtung gleiches Gewicht haben.

Ziel ist also eine möglichst kleine Maximalbeschleunigung in X- und Y-Richtung.

Sie werden sehen, wie wir die Beschleunigung in diesem Beispiel von 125.7 m/s2 auf 17 m/s2 verringern können.

Bewegungsauslegung 1:

Eine erste Bewegungsauslegung könnte so aussehen:

• konsequente Folge-Programmierung der Einzelbewegungen (wie bei NC-Achsen üblich)
• mit dem beliebten Bewegungsgesetz "Geneigte Sinuslinie"
• und freier Verteilung der Übergangszeiten
• mit Ausnutzung des vollen Vertikalhubes

"Folge-Programmierung" bedeutet, dass eine Bewegungsphase (öffnen, schließen, auf, ab, links, rechts) erst starten darf, wenn die logisch vorhergehende Bewegung beendet ist. Bei NC-Steuerungen können damit sichere Abläufe programmiert werden, denn ein Schritt wird erst gestartet, wenn die vorhergehende Schritt erfolgreich beendet wurde.

Es ergeben sich folgende Maximalbeschleunigungen:

In Horizontalrichtung X:

amax_x =  90.5 m/s2

In Vertikalrichtung Y:

amax_y = 125.7 m/s2

Diese Maximalbeschleunigungen finden Sie in den folgenden Diagrammen immer links am Rand und in roter Farbe.

Bewegungsauslegung 2:

Sinnvoll ist es, die Symmetrieeigenschaften des Bewegungsplans zu berücksichtigen:

• horizontales Hin- und Zurückfahren sollten gleich lang dauern
• alle Vertikalhübe sollten gleich lang dauern

Ergebnis:

amax_x =  35.3 m/s2
amax_y = 125.7 m/s2
 

Bewegungsauslegung 3:

Im nächsten Schritt wollen wir überlegen, ob die geneigte Sinuslinie das richtige Bewegungsgesetz ist. Es hat einen großen Beschleunigungskennwert (Ca = 6.283). Den theoretisch kleinsten Ca-Wert für R-R-Anwendungen besitzt die Quadratische Parabel (Ca = 4), aber sie ist ruckbehaftet. Obwohl das Polynom 8. Grades mit Ca = 4.667 einen kleineren Beschleunigungskennwert aufweist, wollen wir uns für das Modifizierte Beschleunigungstrapez mit Ca = 4.888 entscheiden, weil der Maximalwert der Ruckfunktion kleiner ist.

Ergebnis mit Bewegungsgesetz "Modifiziertes Beschleunigungstrapez":

amax_x =  27.5 m/s2
amax_y =  97.8 m/s2
 

Bewegungsauslegung 4:

Weiterhin ist einzurechnen, dass der Vertikalhub (50 mm) halb so gross ist wie der Horizontalhub (100 mm) und deshalb bei gleichen Übergangswinkeln ("Taktwinkelstrecken") halb so große Beschleunigungen hervorruft. Um in X und Y gleiche Beschleunigungen hervorzurufen, sollten die Übergangswinkel von X und Y ins richtige Verhältnis zueinander gesetzt werden.

Die Horizontalwege sollten in ca. 58 Grad Taktwinkel und die Vertikalwege in ca. 41 Grad Taktwinkel zurückgelegt werden, damit sich ausgewogene Beschleunigungswerte ergeben:

amax_x =  52.3 m/s2
amax_y =  52.3 m/s2
 

Bewegungsauslegung 5:

Aus dem Bewegungsdesign ist die Technik "Bereichserweiterung" bekannt.

Wenn wir eine kleine Toleranz von 0.5 mm für die Greiferposition in X und Y bei allen theoretischen Übergangspunkten zulassen und die einzelnen Bewegungen entsprechend eher anfangen und später enden lassen, verringern sich die Beschleunigungen weiter:

amax_x =  38.1 m/s2
amax_y =  41.6 m/s2
 

Bewegungsauslegung 6:

Schließlich müssen wir feststellen, dass wir nach der Bewegungsgesetzauswahl, der ausgewogenen Verteilung der Zeiten und der Bereichserweiterung viel Optimierungspotenzial noch nicht ausgenutzt haben:

• Beim Herausziehen des Stifts aus dem Magazin und beim Montieren muss der Stift und damit der Greifer nur über 30 mm genau senkrecht fahren, nicht über fast 50 mm Gesamtweg.
• Nach dem Beginn des jeweiligen Öffnens muss der Greifer nur näherungsweise senkrecht fahren. Es darf Abweichungen in Horizontalrichtung geben, wenn Greifer und Stift sich nicht berühren.
• Die Vertikalbewegungen dürfen sich eventuell mit den Öffnungs- und Schließbewegungen des Greifers überschneiden. Der Greifer soll in  Aufnahme- und Abgabeposition wirklich stehen, wenn der Greifer weniger als halb geöffnet ist.

Mit diesen Punkten und ausgewogener Neuverteilung der Zeiten erhalten wir folgendes Ergebnis:

amax_x =  17.0 m/s2
amax_y =  16.5 m/s2

Am Bewegungsdiagramm fällt auf, dass wieder eine Asymmetrie hineingekommen ist. Das liegt an den unterschiedlichen Längen 30 mm bzw. 14 mm, die der Greifer exakt bzw. näherungsweise senkrecht fahren muss.

Bei der Leerfahrt zurück kann man auf die kleine Rast in der Position Y=max verzichten und statt dessen einen Umkehrpunkt einsetzen.
Der Vertikalhub 50 mm muss bei der Leerfahrt nicht voll ausgenutzt werden. Optimale Beschleunigungen ergeben sich bei einem etwas kleineren Vertikalhub.

Bis hierher lief die Optimierung ziemlich bequem, hauptsächlich durch Verschieben von Stützpunkten 5-, 2- oder 1-Grad-weise auf der Zeitachse.
Die letzten Feinheiten der Optimierung, die amax_x und amax_y noch genauer gleich setzen und vermutlich auch noch wenige Zehntel m/s2 drücken würden, spielen sich dann in noch kleineren Schrittweiten der Optimierung ab und bringen bei gleichem Aufwand immer kleinere Performance-Steigerungen.

Deshalb soll die Optimierung an dieser Stelle beendet werden. Das Ergebnis kann sich sehen lassen.

Fazit:

Wir sind gestartet mit einer ersten Auslegung "aus dem Bauch heraus" und hatten eine Maximalbeschleunigung von 125.7 m/s2.

Durch klassische Methoden des Bewegungsdesign haben wir die Beschleunigung bis auf 41.6 m/s2 senken können (Auslegung 5), was beachtlich ist.

Die Kollisionsoptimierung hat die Beschleunigung dann noch viel weiter auf 17 m/s2 verringert, und das ist schon der Hammer.

Zum Abschluß der kollisionsoptimierte Bewegungsablauf als Animation:

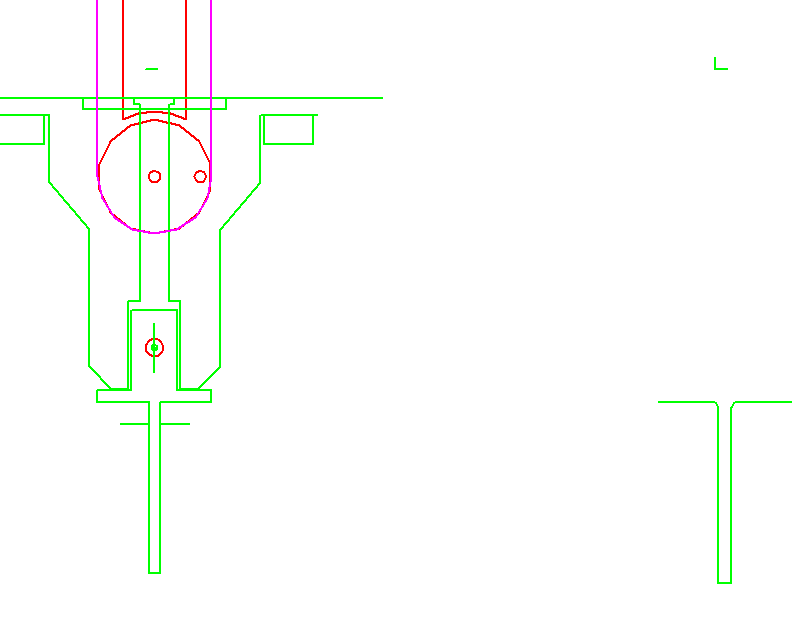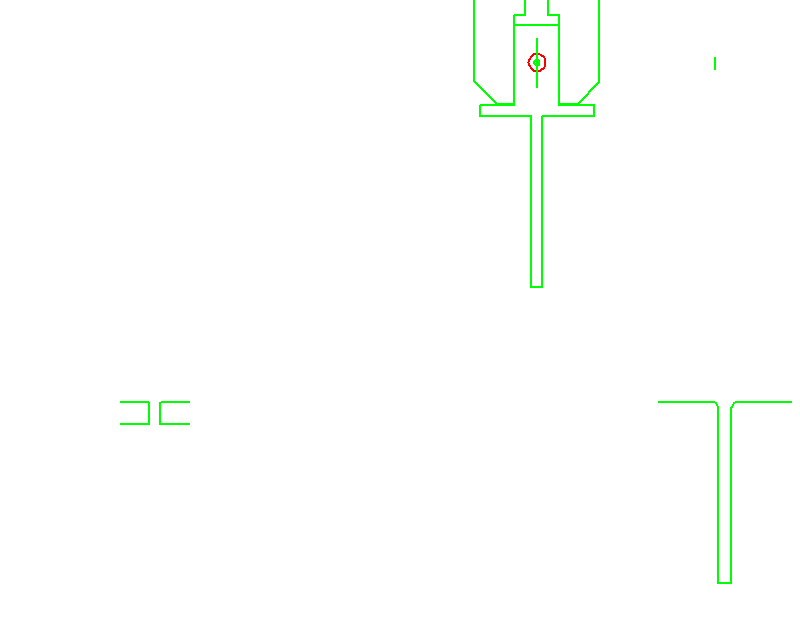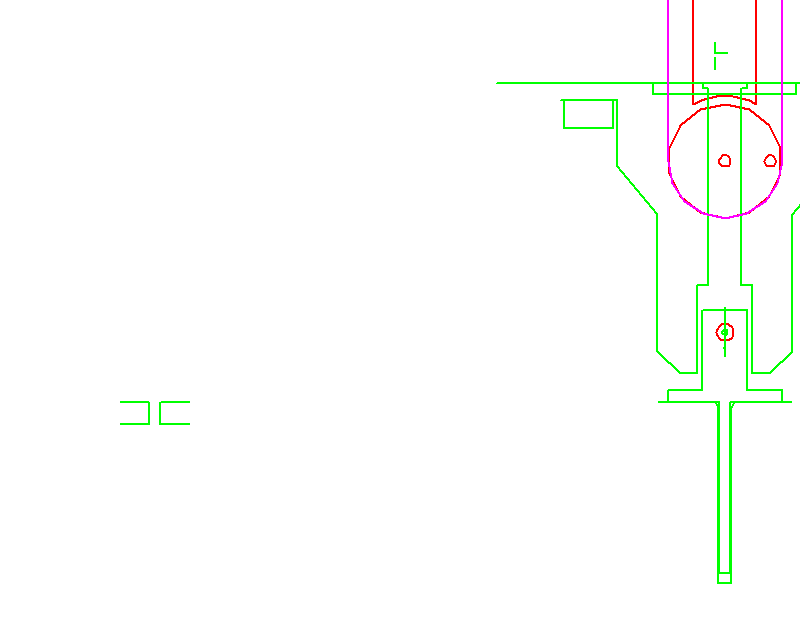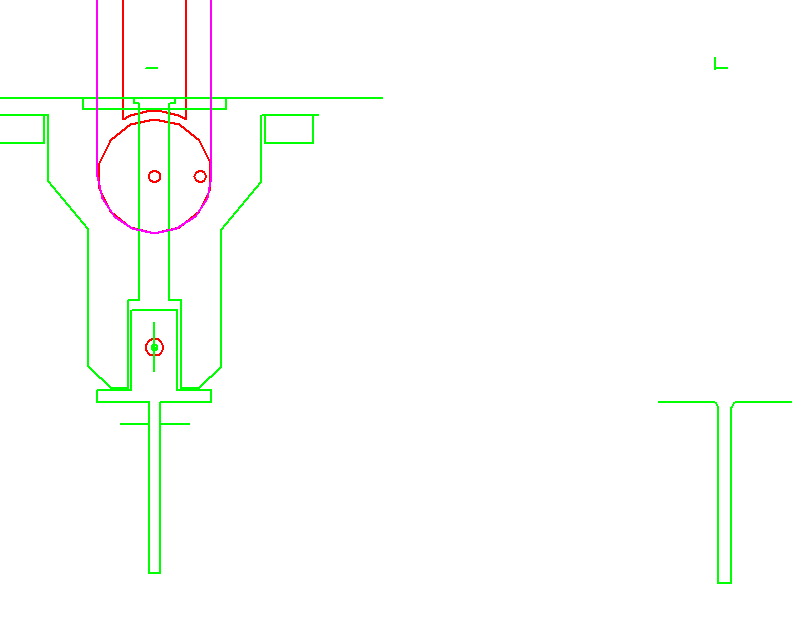
zur Startseite von Nolte NC-Kurventechnik GmbH

Start Fachberichte Mechanismen Kinematik Kurvengetriebe Schrittgetriebe Servo/SPS Bewegungsdesign Fortbildung Software Service Kurvenberechnung Impressum Datenschutz

Allgemeines Spezielleres RichtigesWerkzeug Faltung Sammelscheibe Biegeautomat Buchstapler Durchlaufteile Beleimung PnP_Performance 

> zu unseren Kontaktdaten